Torus bifurcations and chaos

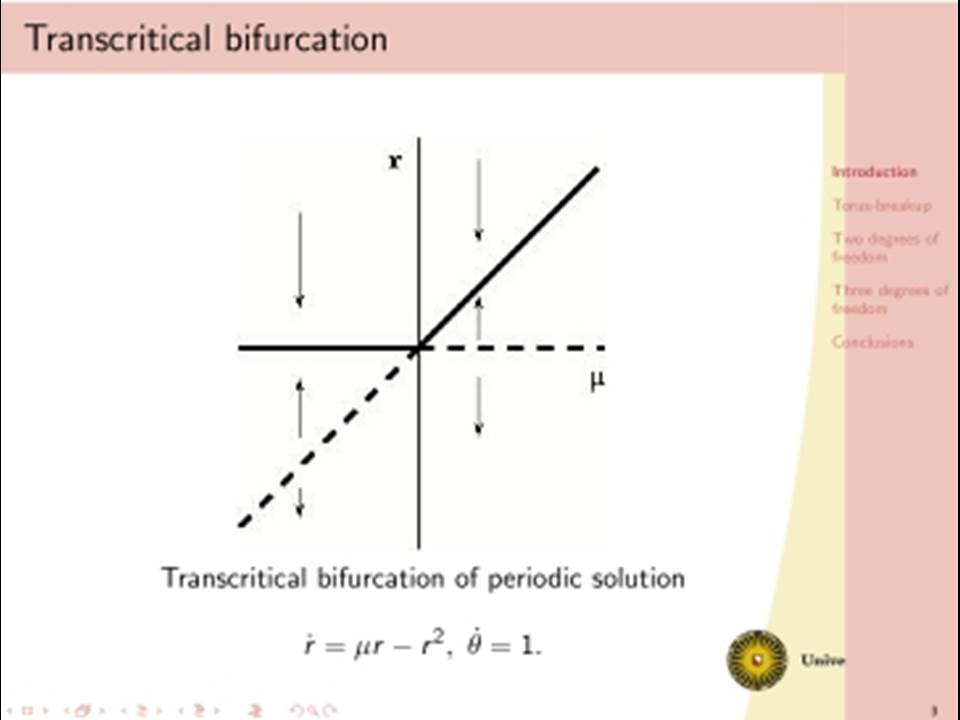
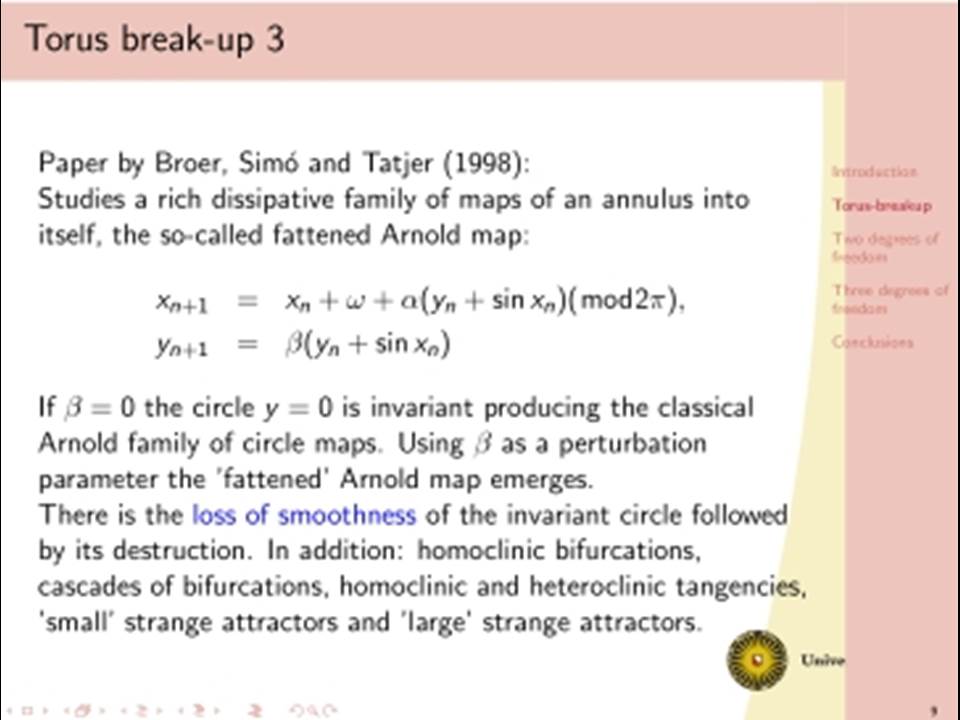
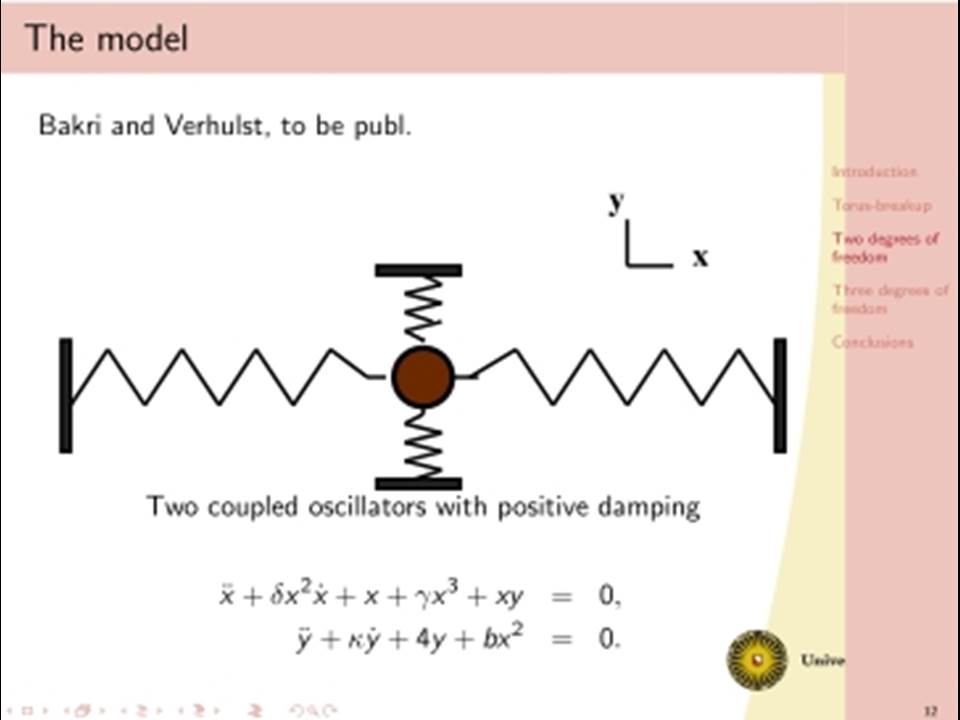
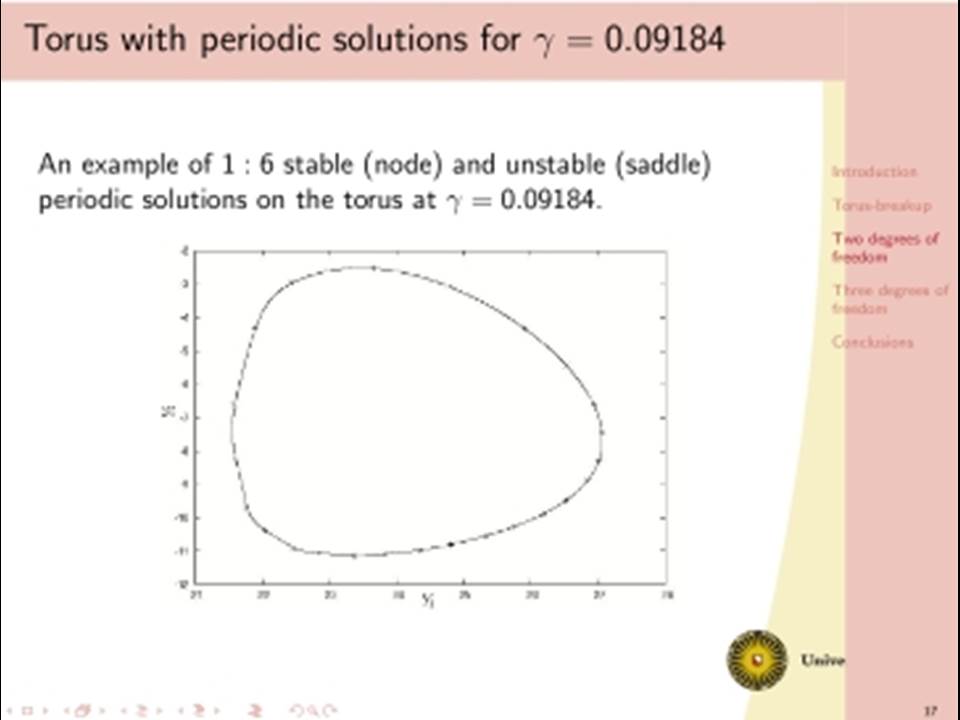
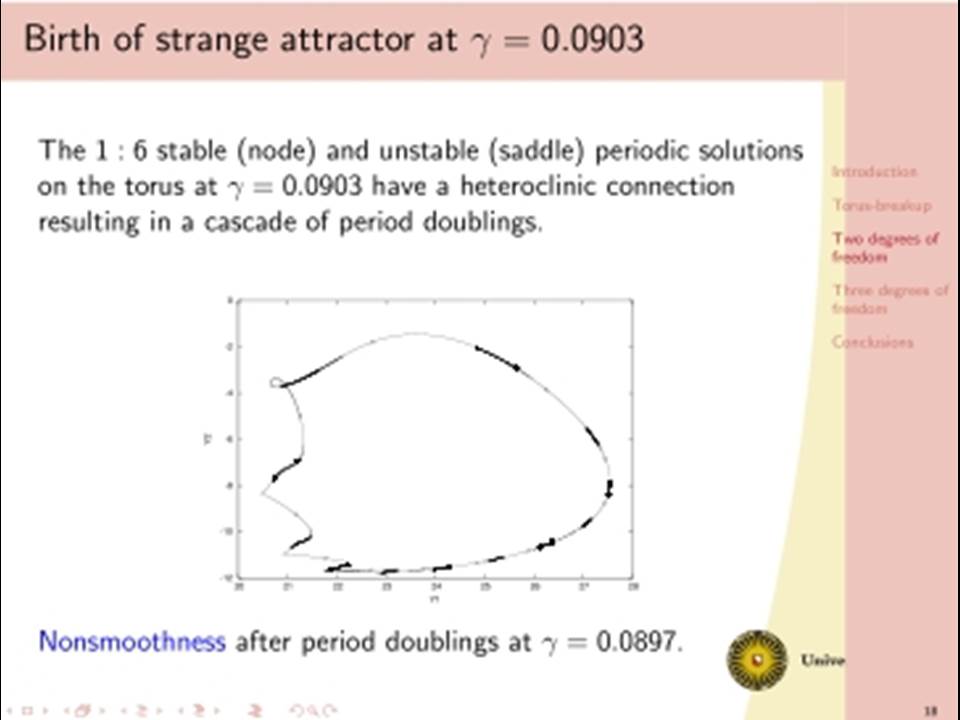
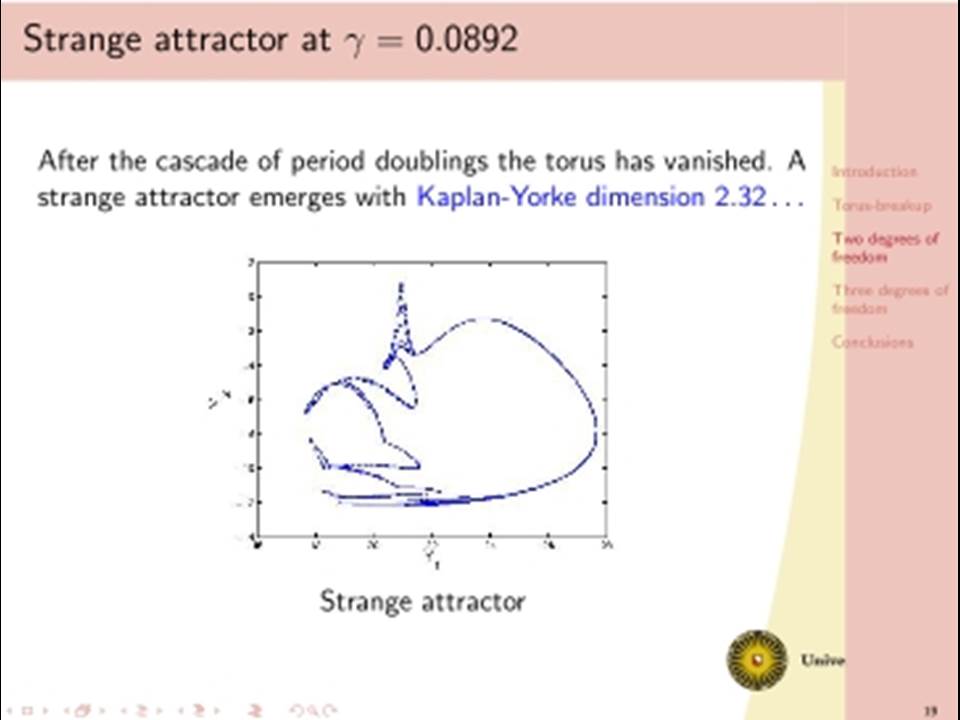
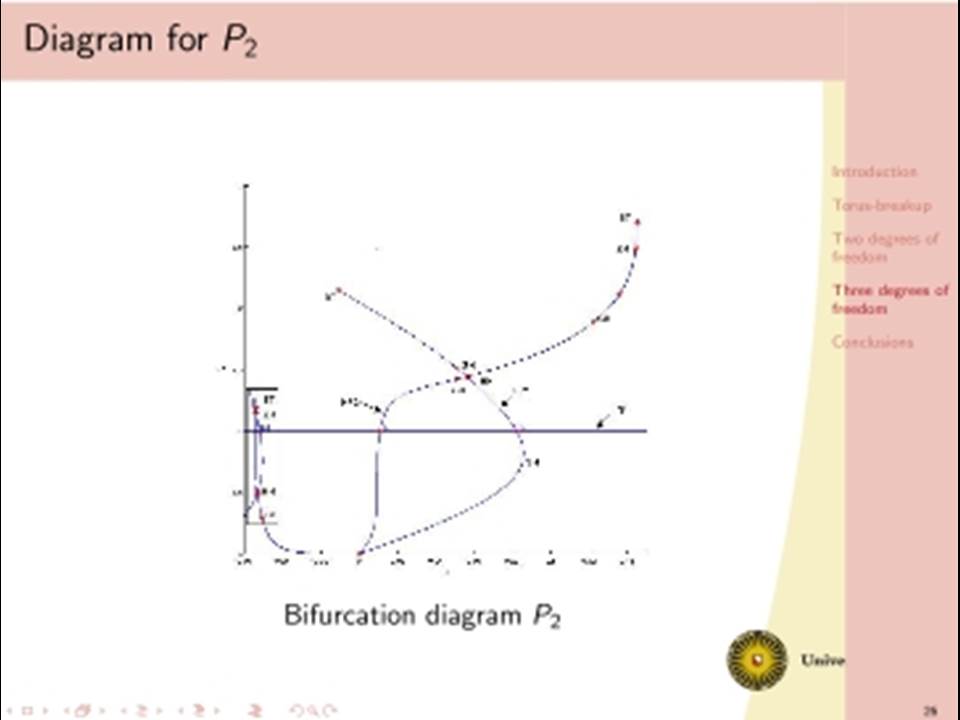
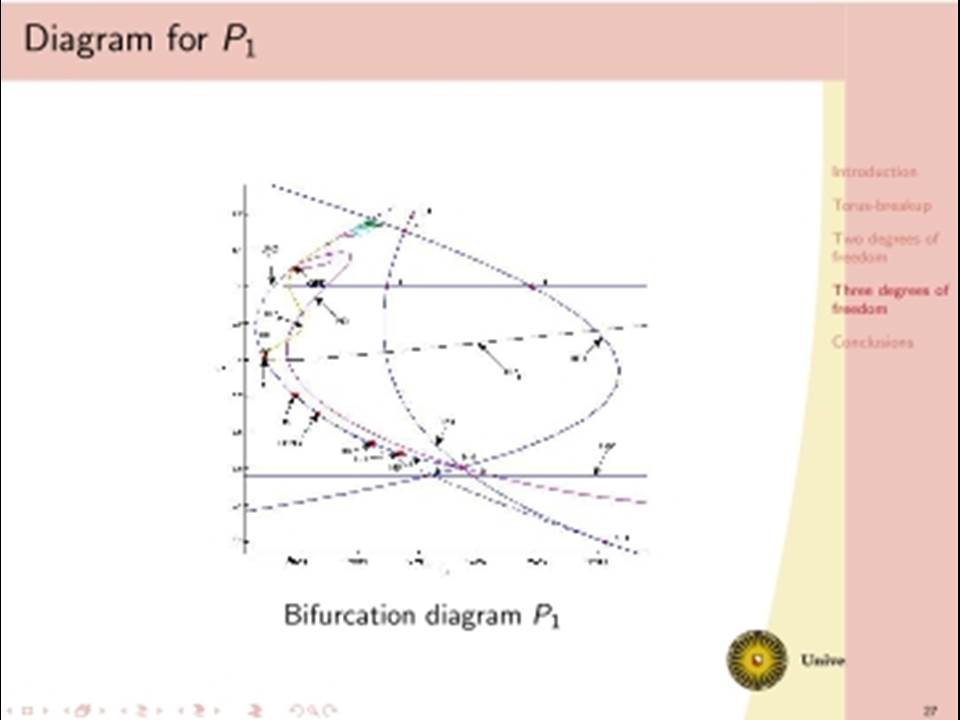
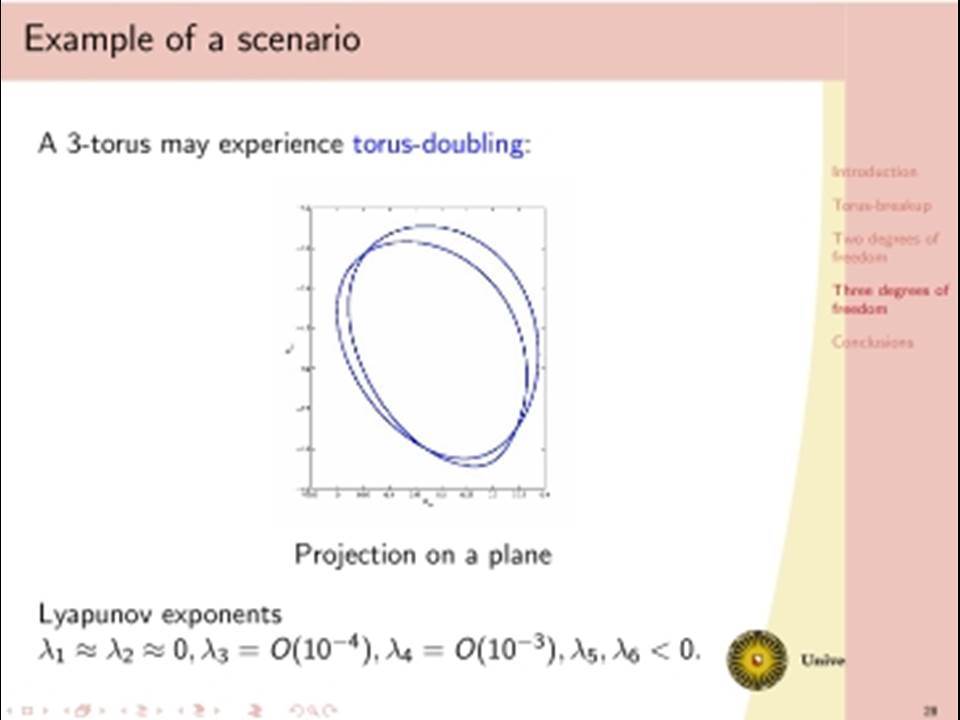
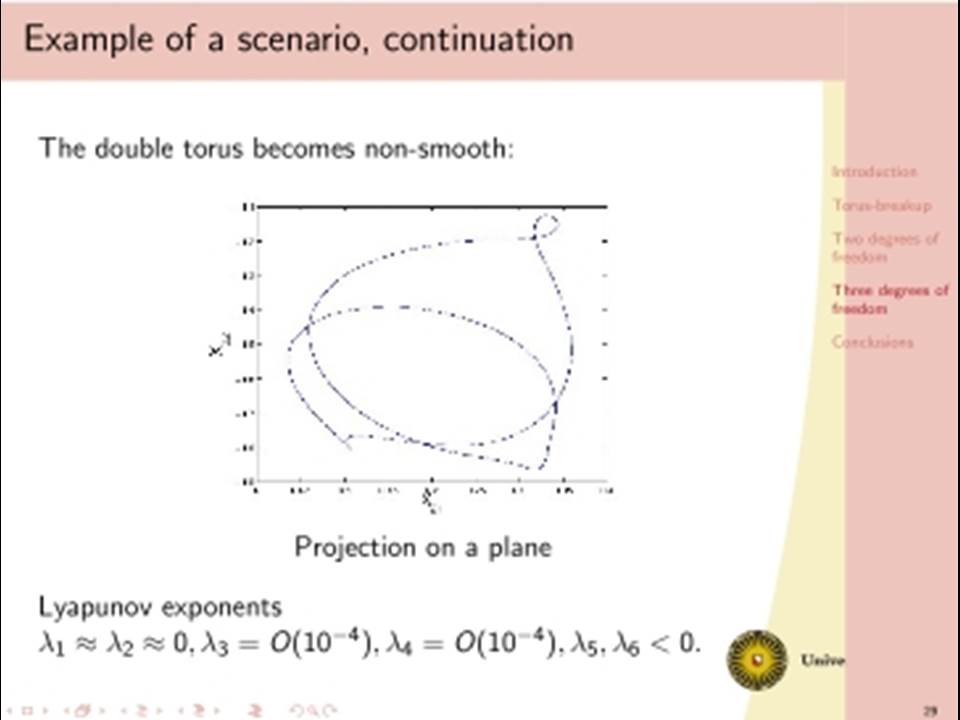
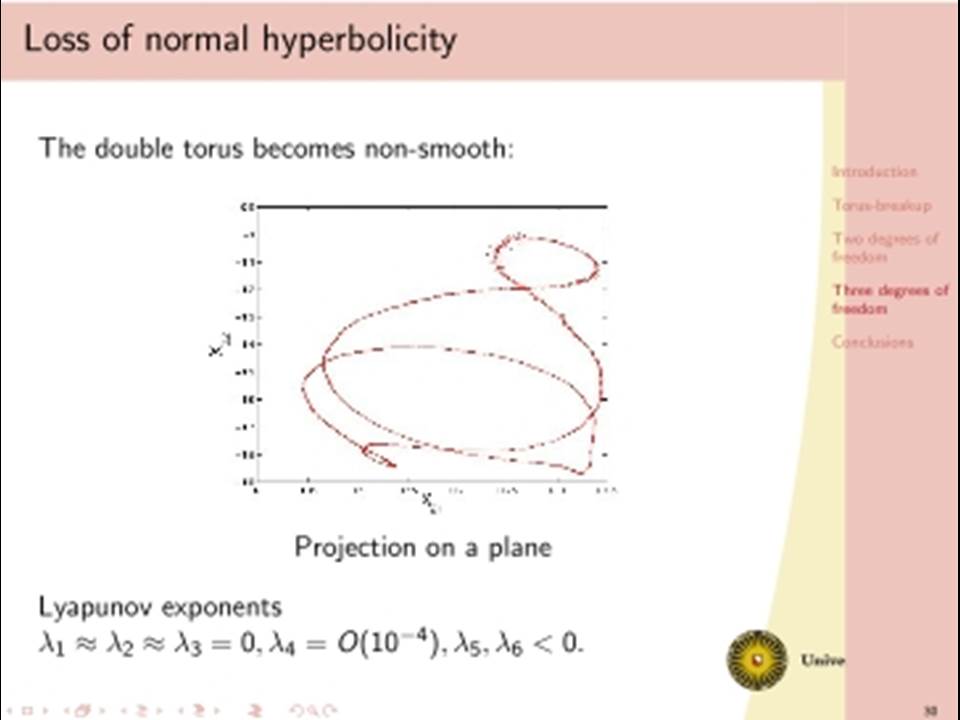
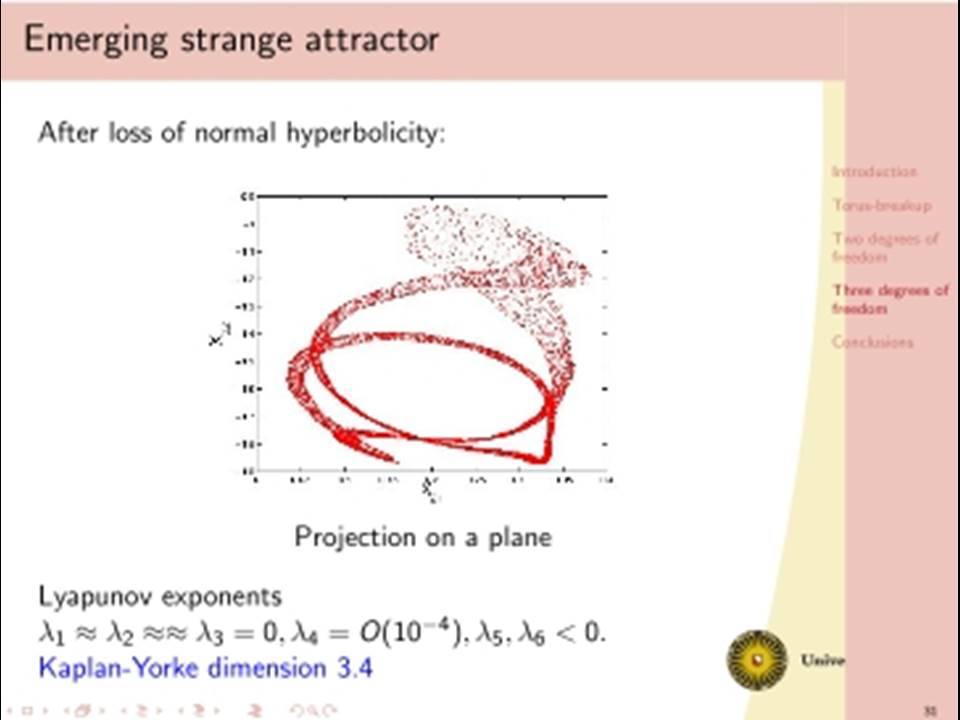
The classical analysis of dissipative dynamics focuses on finding equilibria and periodic solutions and their stability. Considering systems with more than one degree of freedom, such as interacting nonlinear oscillators, this analysis must be supplemented by a study of quasi-periodic solutions and their bifurcations. Geometrically, quasi-periodic solutions correspond with tori, for instance two-frequency oscillations typically describe motion on a two-torus. It turns out that geometric visualisation improves our understanding of the basic dynamics as bifurcational changes of the dynamics will correspond with changes in the geometry and vice versa. We will consider models with two or three interacting oscillators. Under specific conditions a periodic solution of such a two dof system undergoes a Neimark-Sacker bifurcation producing a torus. In one physically simple model, after the Neimark-Sacker bifurcation has occurred, we will focus on the dynamics within the 1:6 resonance tongue. Through one route in the parameter space, the torus becomes nonsmooth before it breaks down, leading to a large strange attractor. This loss of smoothness occurs before the phase locked periodic solution has lost normal hyperbolicity and has undergone one period doubling. Hereafter a cascade of period doublings in the 1:6 resonant tongue in the direction orthogonal to the unstable manifolds of the saddles follows, after which a nontrivial limit set emerges and a strange attractor is born. In addition we will discuss a (simple looking) 3 dof system with even more complicated bifurcational behaviour.