























Sokolov Valentin
Γλώσσα
Αγγλική
Ημερομηνία
12/06/2012
Διάρκεια
38:11
Εκδήλωση
5th Chaotic Modeling and Simulation International Conference (CHAOS2012)
Χώρος
Ξενοδοχείο President
Διοργάνωση
Χρήστος Σκιαδάς
Κατηγορία
Μαθηματικά, Φυσικές επιστήμες
Possible mechanisms are discussed of suppression of the quantum interference ("decoherence"). Being, in essence, of quite general nature, this question takes on special significance for understanding the quantum-classical correspondence in the non-trivial case of non-linear classically chaotic quantum systems. Though the rapid decay of phase correlations is an underlying feature of the classical dynamical chaos, so called "quantum chaos" is not, by itself, capable of destroying the quantum phase coherence. Basically, formation of incoherent mixed states is necessary for decoherence to appear. Therefore interaction with a disordered environment plays a primary role.
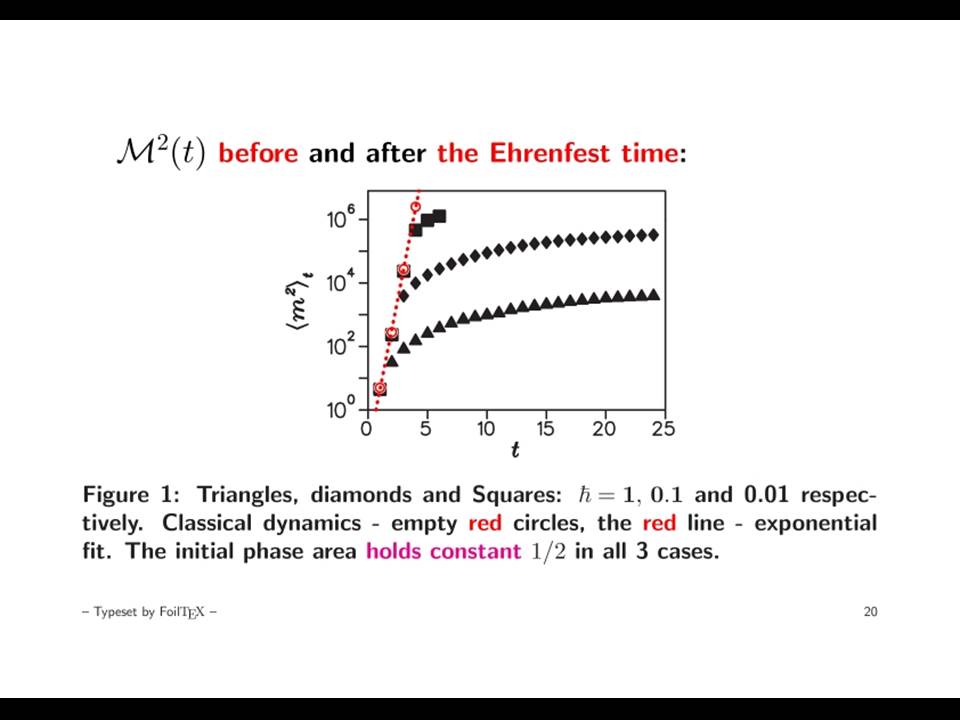
Exponential sensitivity of classical chaotic systems to any external influence makes at bottom impractical the very treatment of such systems as closed ones. Inevitably, arbitrarily weak interaction with environment crucially influences the motion. This influence can typically be considered as a noise, that turns the motion into an irreversible random process. Quite opposite, the quantum dynamics of the same systems manifest a considerable degree of stability against external perturbations. This important difference results from the crucial distinction between complexities of the classical and quantum states quantitatively characterised by the number of harmonics of the phase space distribution function in the first case and that of the Wigner function in the second case [2, 3]. There also exists an alternative possibility [4] to describe complexity of a quantum state with the Shannon information entropy I(t). It is important to stress that the quantum phases are left aside in both these characteristics.
In both the cases mentioned above sensitivity of the motion to external perturbations is described by the decay of the Peres fidelity or, in other words, the weighted-mean distance between two phase-space distributions (classical or quantum respectively) evolving under two slightly different Hamiltonians. This, in particular, allows one to establish a quantitative relation between the degree of loss of memory on the one hand and complexity (i.e. the number of harmonics) of the corresponding phase-space distribution on the other hand [3]. In the case of classical chaotic dynamics, this number grows exponentially in time with the rate related to the Lyapunov exponent that describes the exponential instability of the classical trajectories. In the meanwhile the number of harmonics of the Wigner function grows only algebraically because of the quantization of the phase space. This explains why the quantum dynamics is much more stable than that of corresponding classical counterpart.
The way the decoherence phenomenon shows up depends on the nature of the quantity considered. Thus in the presence of a stationary noise, the most relevant quantity is the fidelity averaged over the noise realizations [4]. Such a choice brings into consideration the averaged density matrix. Since evolution of the latter is not unitary this entails state mixing and suppression of the quantum interference. The newly defined fidelity depends only on the level (strength) \sigma of the noise. It turns out to be possible to analytically calculate such a quantity in the two limiting cases of very weak (\sigma\ll 1) noise when the perturbation expansion is possible and extremely strong noise (\sigma\gg1) when the evolution becomes Markovian. It is worth noting that the degree of reversibility of the motion under the influence of a stationary noise persisting during the forward as well as the backward evolutions is defined by the purity P(\sigma; t) of the state at the reversal moment t. In the intermediate region the time evolution of the fidelity displays non-trivial scaling behavior.
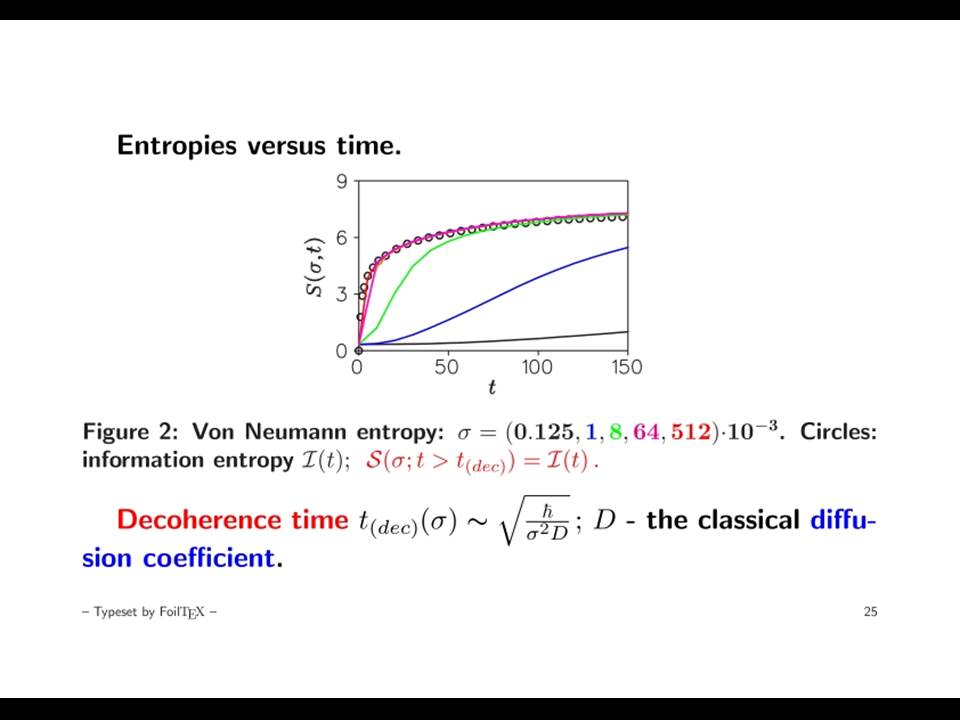
The state mixing induced by the noise leads to loss of the memory on the initial state. Thereupon the notion of the invariant (basis-independent) von Neumann entropy S(\sigma; t) becomes relevant. This entropy is sensitive, unlike the Shennon entropy, to the quantum coherence and therefore remains during evolution smaller than the latter. But in time the von Neumann entropy increases monotonically approaching the information entropy from below. After all they get equal by the moment of time t_{(dec)}(\sigma)=
\sqrt{\frac{6h}{D\sigma^2}} (D is the classical diffusion coefficient). The complete decoherence is reached at that moment while the system occupies the whole phase volume accessible at the running degree of excitation thus reaching a sort of equilibrium. Henceforth the phase volume expands "adiabatically": the entropy remains practically constant.
Another interesting aspect of the problem of decoherence is evoked by Ramsey-type interferometry experiments with periodically kicked ion traps. They suggest a certain generalization of the standard pure-state fidelity to mixed quantum states [1]. This quantity, which we called "allegiance", directly accounts for the quantum interference and can, at first glance, be expected to retain quantal features even in the deep semiclassical domain. It turns out nevertheless that if the evolution of a classically chaotic system starts from a wide and perfectly incoherent mixed state (and any classical device is capable of preparing only such sort of states!), then the initial incoherence persists so that the quantum phases remain irrelevant and the allegiance reduces to an appropriate classical correlation function.
Decoherence during ballistic quantum transport trough a 2D mesoscopic open structure is an issue of great interest from the both, theoretical as well as experimental, points of view. Effects induced by interaction with a complicated many-body environment with a weak disorder [5] is also analysed in this presentation. The temperature of the environment is supposed to be zero whereas the energy of the incoming particle E_in can be close to or somewhat above the Fermi surface in the environment. The doorway resonance states excited in the structure via external channels are damped not only because of escape through such channels but also due to the ulterior population of the long-lived environmental states. Transmission of an electron with a given incoming E_in through the structure turns out to be an incoherent sum of the flow formed by the interfering damped doorway resonances and the retarded flow of the particles re-emitted into the structure by the environment. Though the number of the particles is conserved in each individual event of transmission, there exists a probability that some part of the electron's energy can be absorbed due to environmental many-body effects thus violating the time-reversal symmetry and, as a consequence, suppressing the weak localization phenomenon. Besides the electron can disappear from the resonance energy interval and elude observation at the resonant transmission energy Ein imitating thereby loss of the particles. The both decoherence and absorption phenomena are treated within the framework of a unit microscopic model based on the general theory of the resonance scattering. All the effects discussed are controlled by the only parameter: the spreading width of the doorway resonances, that uniquely determines the decoherence rate.
[2] Valentin V. Sokolov, Oleg V. Zhirov, Giuliano Benenti, Giulio Casati, Phys. Rev. E 78 (2008) 046212.
[3] Valentin V. Sokolov, Oleg V. Zhirov. Quantum Chaos: How Well a Quantum System Can Retain Memory of Its Initial State? Europhys. Lett. 84 (2008) 30001.
[4] Valentin V. Sokolov, Oleg V. Zhirov, and Yaroslav A. Kharkov, Quantum Dynamics Against a Noisy Background, Europhys. Lett. 88 (2009) 60002.
[5]Ya.A. Kharkov, V.V. Sokolov and O.V. Zhirov, Quantum chaos versus noisy environment, J. Sib. Fed. Univ. Math. Phys., 2010, Volume 3, Issue 3, Pages 303-310.
[6] Valentin V. Sokolov, Ballistic electron Quantum transport in a presence of a disordered background, J. Phys. A: Math. Theor. 43 (2010) 265102.

